前回は、統計学における中心の尺度として、「平均」、「中央値」、「最頻値」について説明しました。今回は、この3つの値から読み取れるデータ分布の特徴について説明します。また、前回説明したPythonのグラフ描画ライブラリ「matplotlib」を使用してグラフを表示し、視覚的に捉えてみましょう。
中心の尺度の関係
平均と中央値、最頻値の値を比較するだけで、そのデータ分布がどのように歪んでいるかをおおまかに把握することができます。
データ分布の歪み
例えば、最頻値 < 中央値 < 平均 となるデータ分布を考えてみましょう。最頻値や中央値よりも平均が大きいということは、少数の大きな値を持つ要素が平均を引き上げていることが考えられます。この場合、データ分布は「右に歪んだ」状態になります。
最頻値 < 中央値 < 平均 = 右に歪んだ分布
対して、平均 < 中央値 < 最頻値 となるデータ分布は、右に歪んだ状態とは逆で、少数の小さな値が平均を引き下げていると考えられます。つまり、「左に歪んだ」データ分布となります。
平均 < 中央値 < 最頻値 = 左に歪んだ分布
matplotlibでグラフを表示する
では、matplotlibを使ってグラフを表示して、データ分布の歪みを視覚的に確認してみましょう。
平均 = 中央値 = 最頻値となる分布
以下のコードは、0から100の値を取り得る中で、平均と中央値、最頻値がすべて50となるデータのグラフを描画する例です。例えば、何かの試験の点数分布みたいなデータですね。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 1.配列を作成する
data = np.array([10, 20, 30, 40, 50, 50, 60, 70, 80, 90])
# 2.中心の尺度を確認する
# 平均の表示
print(data.mean())
# 中央値の表示
print(np.median(data))
# 最頻値の表示
print(stats.mode(data)[0])
# 3.等差数列を作成する
x = np.arange(0, 100, 1 / 1000)
# 4.正規分布の確率密度関数(scipy.stats.norm.pdf)データ配列と平均、標準偏差を渡して確率分布を取得する
y = stats.norm.pdf(x, data.mean(), data.std())
# 5.グラフを描画する
# 作成した等差数列をx軸に、確率分布をy軸としてグラフを作成する
plt.plot(x, y)
# 表示するグラフのx軸の範囲を指定する
plt.xlim([0, 100])
# x軸のラベルをデータ配列の数値にする
plt.xticks(data)
# y軸の目盛りを非表示にする
plt.yticks(color="None")
plt.tick_params(length=0)
# グラフを表示する
plt.show()簡単にコードを解説します。
- 配列を作成する
ndarrayクラスでデータの配列を取得します。 - 中心の尺度を確認する
前回の記事で解説した方法で平均、中央値、最頻値を確認します。 - 等差数列を作成する
取り得る値(0から100)の範囲で、その範囲で1000分の1刻みの差となる等差数列を作成します。 - 確率分布を取得する
確率密度関数(scipy.stats.norm.pdf)に等差数列と平均、標準偏差を渡して確率分布を取得します。ここが少し理解しにくいかもしれません。 - グラフを描画する
X軸にデータの配列を、Y軸に確率分布を渡して、グラフを作成します。グラフのデザインは、pyplotの値をプロパティを操作することで変更できます。
4の部分が、少し理解しにくいかもしれません。要は、配列のそれぞれの値を確率密度関数で計算し、それぞれの値が発生する確率を計算しています。詳細は、後々の記事で解説しようと思います。今回はあくまでデータ分布の歪みを確認することが目的なので、深入りしません。
上記のコードを実行することで、以下の結果が得られます。
50.0
50.0
[50]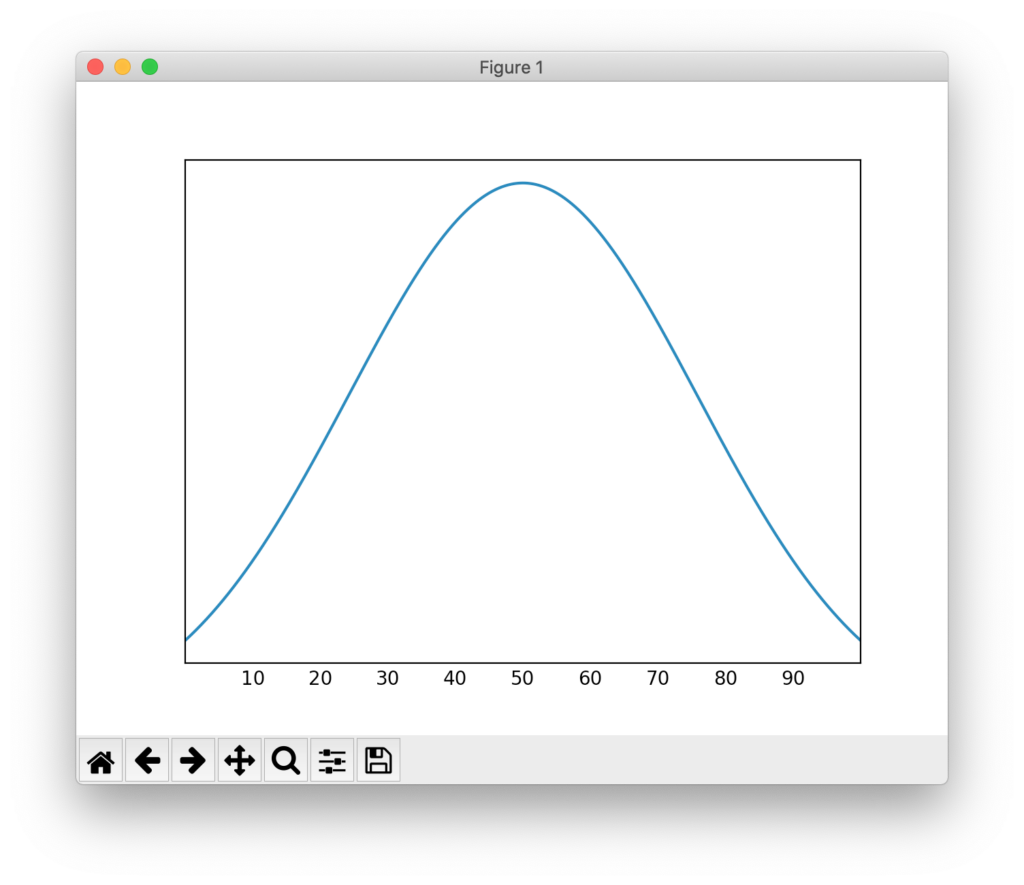
平均、中央値、最頻値がすべて等しいことと、左右対称なグラフが描画されることを確認できます。
平均 < 中央値 < 最頻値となる分布
続いて、平均値 < 中央値 < 最頻値となる分布のグラフを見てみましょう。なお、グラフの描画など、繰り返し利用するので、以下のコードではDataクラスを作成しています。基本的な処理の流れは、先ほどのコードと違いはありません。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
class Data:
def __init__(self, input_data):
self.data = input_data
@property
def data(self):
return self.__data
@data.setter
def data(self, input_data):
self.__data = np.array(input_data)
def print_mean(self):
print(self.data.mean())
def print_median(self):
print(np.median(self.data))
def print_mode(self):
print(stats.mode(self.data)[0])
def show_graph(self, input_min, input_max):
__x = np.arange(input_min, input_max, 1 / 1000)
__y = stats.norm.pdf(__x, self.data.mean(), self.data.std())
plt.plot(__x, __y)
plt.xlim([input_min, input_max])
plt.xticks(self.data)
plt.yticks(color="None")
plt.tick_params(length=0)
plt.show()
# Dataクラスをインスタンス化する
data = Data([10, 20, 30, 40, 50, 60, 70, 80, 90, 90, 90, 90, 90])
# 平均、中央値、最頻値を出力する
data.print_mean()
data.print_median()
data.print_mode()
# グラフを描画する
data.show_graph(0, 100)実行すると以下の結果が得られます。
62.30769230769231
70.0
[90]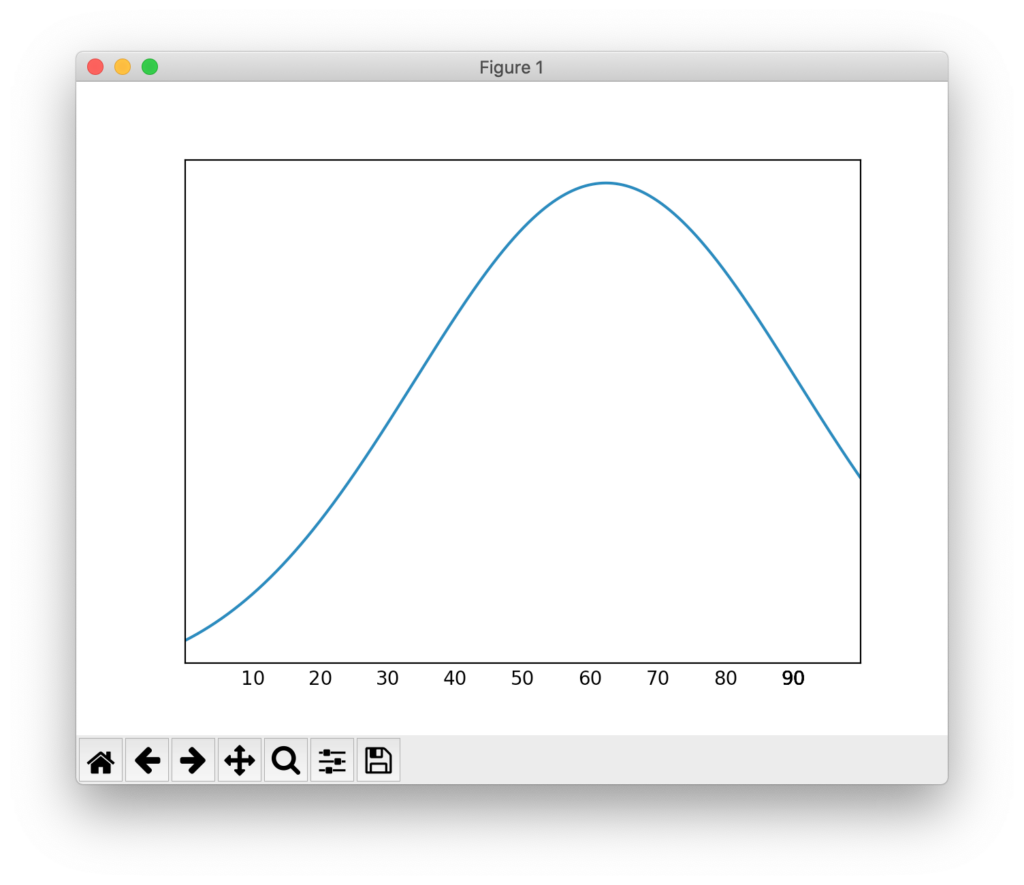
平均が62、中央値が70、最頻値が90となり、グラフが右に歪んでいることがわかります。
最頻値 < 中央値 < 平均となる分布
続いて、最頻値 < 中央値 < 平均となる分布のグラフを描画してみます。Dataクラスを引き続き利用します。
# Dataクラスをインスタンス化する
data = Data([10, 10, 10, 10, 10, 20, 30, 40, 50, 60, 70, 80, 90])
# 平均、中央値、最頻値を出力する
data.print_mean()
data.print_median()
data.print_mode()
# グラフを描画する
data.show_graph(0, 100)これを実行すると、以下の結果が得られます。
37.69230769230769
30.0
[10]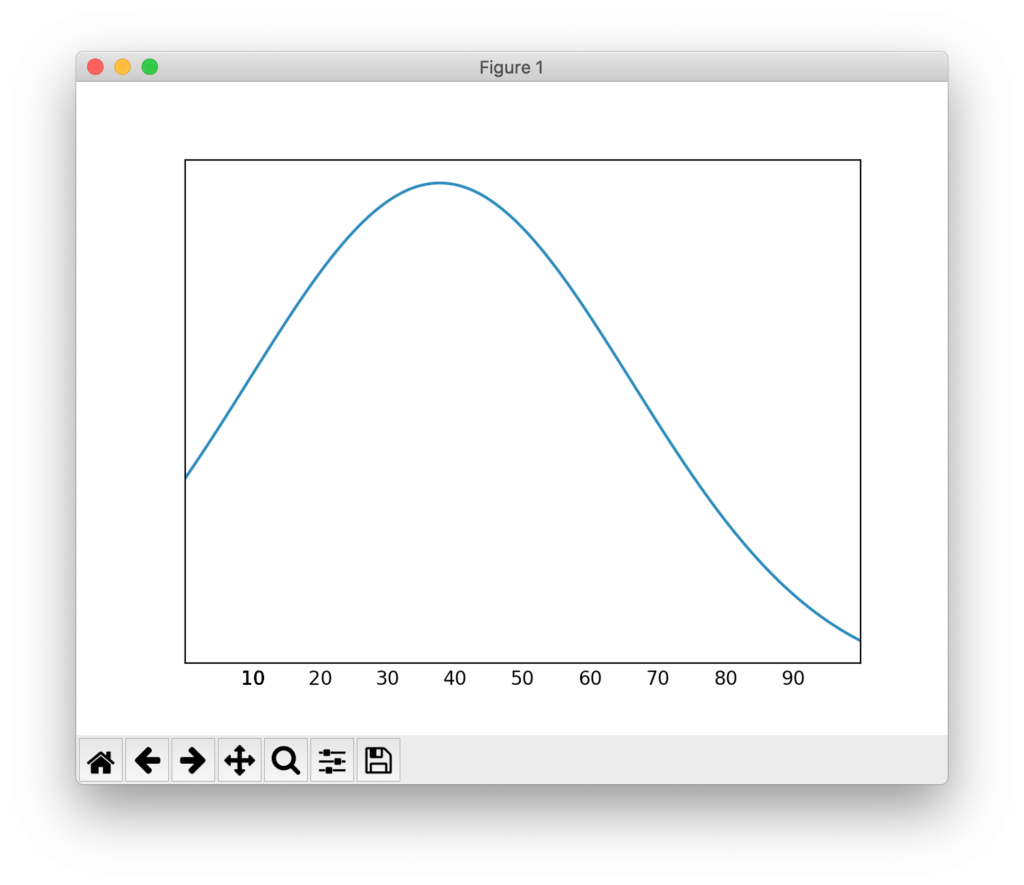
今度は平均が37、中央値が30、最頻値が10となります。グラフが左に歪んでいることがわかります。
今回のまとめ
今回は平均、中央値と最頻値の関係によって、データ分布がどのように変化するかを確認しました。この3つの値に着目するだけでも、おおまかにどのようなデータ分布であるかを見出すことができました。
次回は、別の観点から見る尺度として、散らばりの尺度について解説しようと思います。


コメント