今回から、統計学にて、データ分布を視覚的に捉える方法と、それをPythonで実装する方法について解説します。具体的には、度数分布表やヒストグラムと言った表やグラフで表現します。また、Pythonで度数分布表やヒストグラムを表示するために、新たにライブラリ「Pandas」を使用するので、こちらについても解説を加えます。
データ解析ライブラリ「Pandas」
Pandasとは、Pythonで利用できるデータ解析のためのライブラリです。プログラムから生成したデータだけでなく、CSVファイルからデータを読み込むことも可能です。
Pandasの使い方
Pandasでは、配列データやCSVファイルを読み込み、DataFrameクラスをインスタンス化した上で、様々な分析を行うのが、基本的な流れです。以下のコードは、Pandasを使用してCSVファイルを読み込み、その内容を表示するコードです。
import pandas as pd
df = pd.read_csv('../data/c01.csv', encoding='shift-jis', header=0)
print(df.__class__)
print(df)なお、読み込んでいるc01.csvは、e-statにてダウンロードできる「男女別人口-全国, 都道府県(大正9年〜平成27年)」のデータです。実行すると以下のように表示されます。
都道府県コード 都道府県名 元号 和暦(年) 西暦(年) 注 人口(総数) 人口(男) 人口(女)
0 00 全国 大正 9.0 1920.0 NaN 55963053 28044185 27918868
1 01 北海道 大正 9.0 1920.0 NaN 2359183 1244322 1114861
2 02 青森県 大正 9.0 1920.0 NaN 756454 381293 375161
3 03 岩手県 大正 9.0 1920.0 NaN 845540 421069 424471
4 04 宮城県 大正 9.0 1920.0 NaN 961768 485309 476459
.. ... ... ... ... ... ... ... ... ...
977 45 宮崎県 平成 27.0 2015.0 NaN 1104069 519242 584827
978 46 鹿児島県 平成 27.0 2015.0 NaN 1648177 773061 875116
979 47 沖縄県 平成 27.0 2015.0 NaN 1433566 704619 728947
980 1) 沖縄県は調査されなかったため,含まれていない。 NaN NaN NaN NaN NaN NaN NaN NaN
981 2) 長野県西筑摩群山口村と岐阜県中津川市の境界紛争地域人口(男39人,女34人)は全国に含... NaN NaN NaN NaN NaN NaN NaN NaN
[982 rows x 9 columns]データの特徴を視覚的に捉える
それでは、統計学にてデータの特徴を視覚的に捉える方法を説明していきます。
度数分布表
度数分布表とは、データの大きさによっていくつかの階級にグループ分けして、それぞれの階級にデータがいくつ存在するか(これを度数と呼びます)を示す表です。
例えば、1, 5, 6, 8, 2, 7, 1, 3, 9というデータを3階級に分けた度数分布表で表すと、下記のようになります。
| 階級 | 度数 |
| 1〜3 | 4 |
| 4〜6 | 2 |
| 7〜9 | 3 |
では、これをPythonで表示してみましょう。まずNumPyのhistogram関数を使って、階級の区切りと度数の配列を取得した後に、それを元にPandasのDataFrameクラスを生成して、最後にmatplotlibを使って表を描画します。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = np.array([1, 5, 6, 8, 2, 7, 1, 3, 9])
hist, bin_edges = np.histogram(data, bins=3)
df = pd.DataFrame({
'RANK': [str(round(bin_edges[i - 1], 2)) + '~' + str(round(bin_edges[i], 2)) for i in range(1, len(bin_edges))],
'COUNT': [hist for hist in hist]
})
# 階級を確認する
print(df['RANK'].values)
# 度数を確認する
print(df['COUNT'].values)
# 度数分布表を描画する
plt.axis('off')
plt.table(cellText=df.values, colLabels=df.columns, loc='center')
plt.show()上記を実行すると、以下のような結果が表示されるはずです。
['1.0~3.67' '3.67~6.33' '6.33~9.0']
[4 2 3]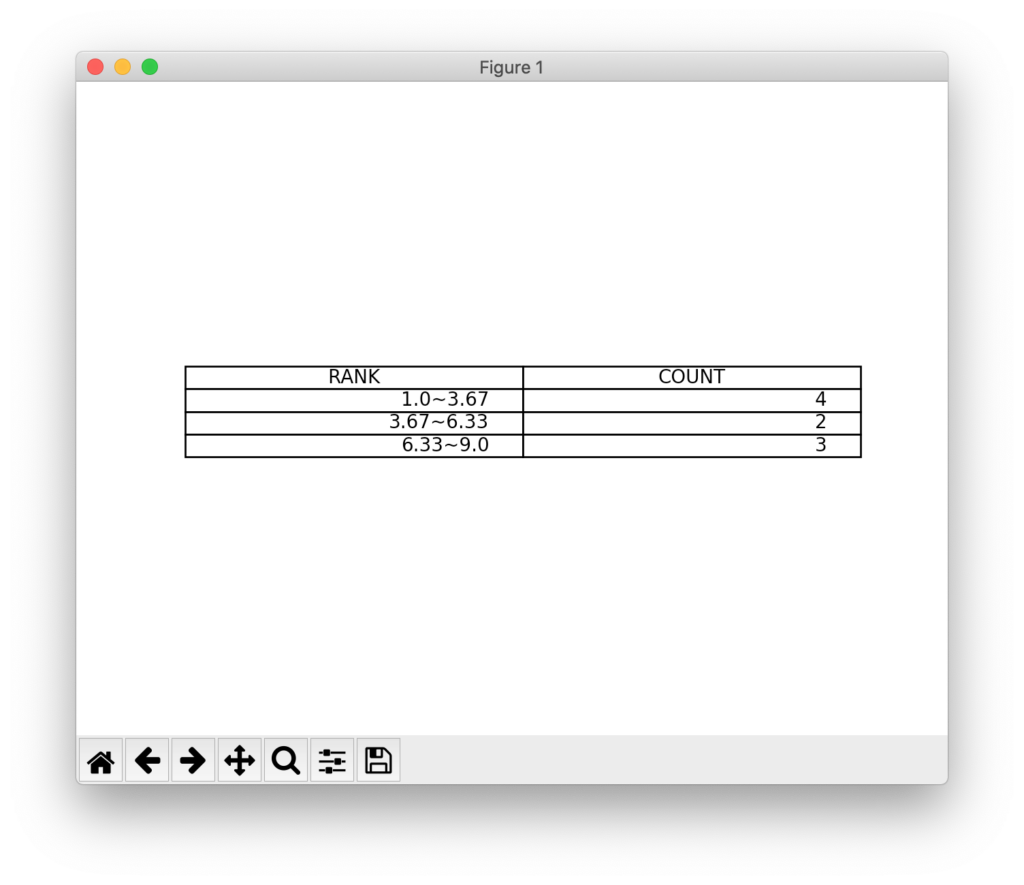
numpy.histogramで取得できる階級は、区切りの値のみになります。そのため、階級を表す文字列に整形して、RANKというカラム名に格納しています。
ヒストグラム
ヒストグラムは、度数分布表を棒グラフで表現したものです。X軸に階級を並べ、Y軸に度数を表示します。Pythonで実装する場合、matplotlibのpyplot.histを使います。下記は、度数分布表とヒストグラムを並べて表示するコードです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = np.random.normal(50, 10, 1000)
hist, bin_edges = np.histogram(data, bins=10)
df = pd.DataFrame({
'RANK': [str(round(bin_edges[i - 1], 2)) + '~' + str(round(bin_edges[i], 2)) for i in range(1, len(bin_edges))],
'COUNT': [hist for hist in hist]
})
# 2行1列のグラフレイアウトを作成する
row = 2
col = 1
plt.figure(figsize=(row*3, col*6))
# 1行目に度数分布表を描画する
plt.subplot(row, col, 1)
plt.axis('off')
plt.table(cellText=df.values, colLabels=df.columns, loc='center')
# 2行目にヒストグラムを描画する
plt.subplot(row, col, 2)
plt.hist(data, bins=10, range=[data.min(), data.max()], histtype='barstacked', ec='black')
plt.show()上記を実行すると、下記の結果が表示されます。
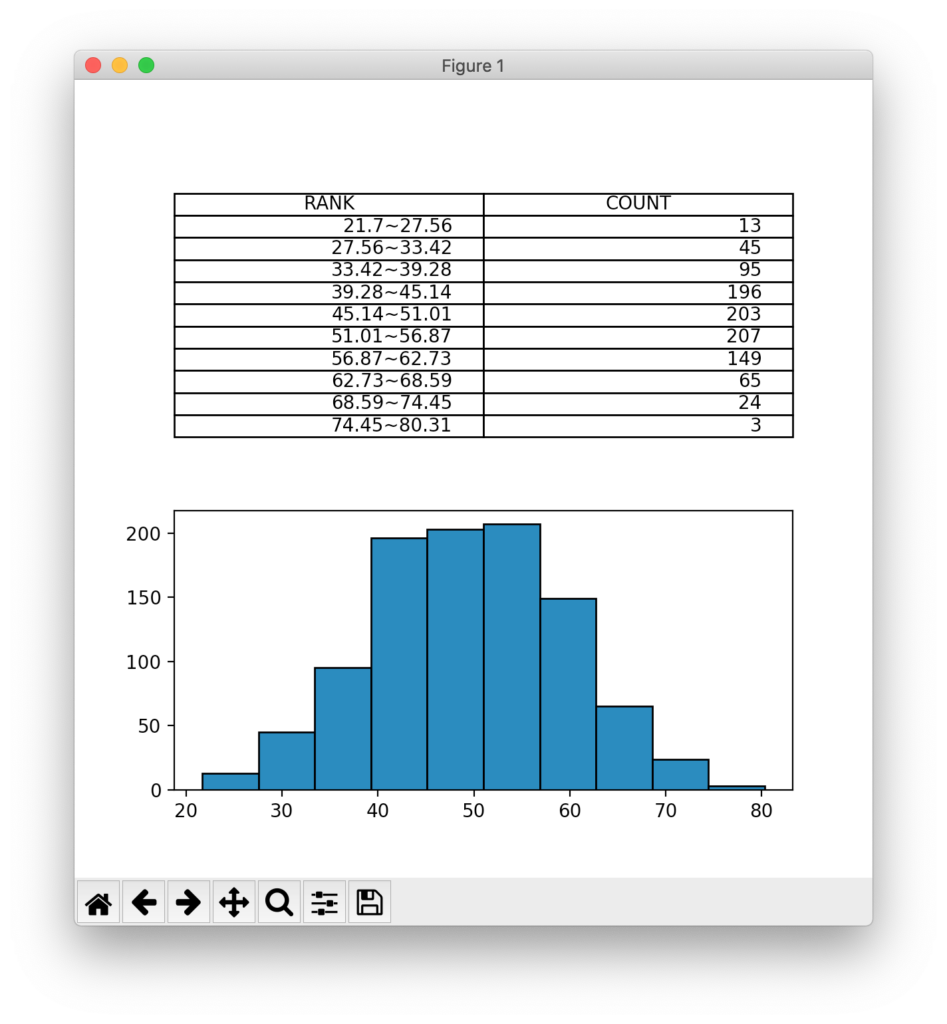
要素の合計数が異なるデータのヒストグラム
複数のデータのヒストグラムを重ねて表現して、データの特徴を比較することはよくあります。例えば、日本全国と、ある特定の1県のデータを比較する場合などです。下記は標準偏差と要素数が異なる2つのデータに関する度数分布表と、そのヒストグラムを重ねて表示するためのPythonコードです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data1 = np.random.normal(50, 10, 1000)
hist1, bin_edges1 = np.histogram(data1, bins=10)
data2 = np.random.normal(50, 15, 10000)
hist2, bin_edges2 = np.histogram(data2, bins=10)
data_all = np.hstack((data1, data2))
df1 = pd.DataFrame({
'RANK': [str(round(bin_edges1[i - 1], 2)) + '~' + str(round(bin_edges1[i], 2)) for i in range(1, len(bin_edges1))],
'COUNT DATA1': [hist for hist in hist1]
})
df2 = pd.DataFrame({
'RANK': [str(round(bin_edges2[i - 1], 2)) + '~' + str(round(bin_edges2[i], 2)) for i in range(1, len(bin_edges2))],
'COUNT DATA2': [hist for hist in hist2]
})
# 3行1列のグラフレイアウトを作成する
row = 3
col = 1
plt.figure(figsize=(row*3, col*9))
# 1行目にデータ1の度数分布表を描画する
plt.subplot(row, col, 1)
plt.axis('off')
plt.table(cellText=df1.values, colLabels=df1.columns, loc='center')
# 2行目にデータ2の度数分布表を描画する
plt.subplot(row, col, 2)
plt.axis('off')
plt.table(cellText=df2.values, colLabels=df2.columns, loc='center')
plt.subplot(row, col, 3)
plt.hist(data1, bins=10, range=[data_all.min(), data_all.max()], histtype='barstacked',
ec='black', alpha=0.3, color='r')
plt.hist(data2, bins=10, range=[data_all.min(), data_all.max()], histtype='barstacked',
ec='black', alpha=0.3, color='b')
plt.show()実行してみると、下記のような画像が表示されます。
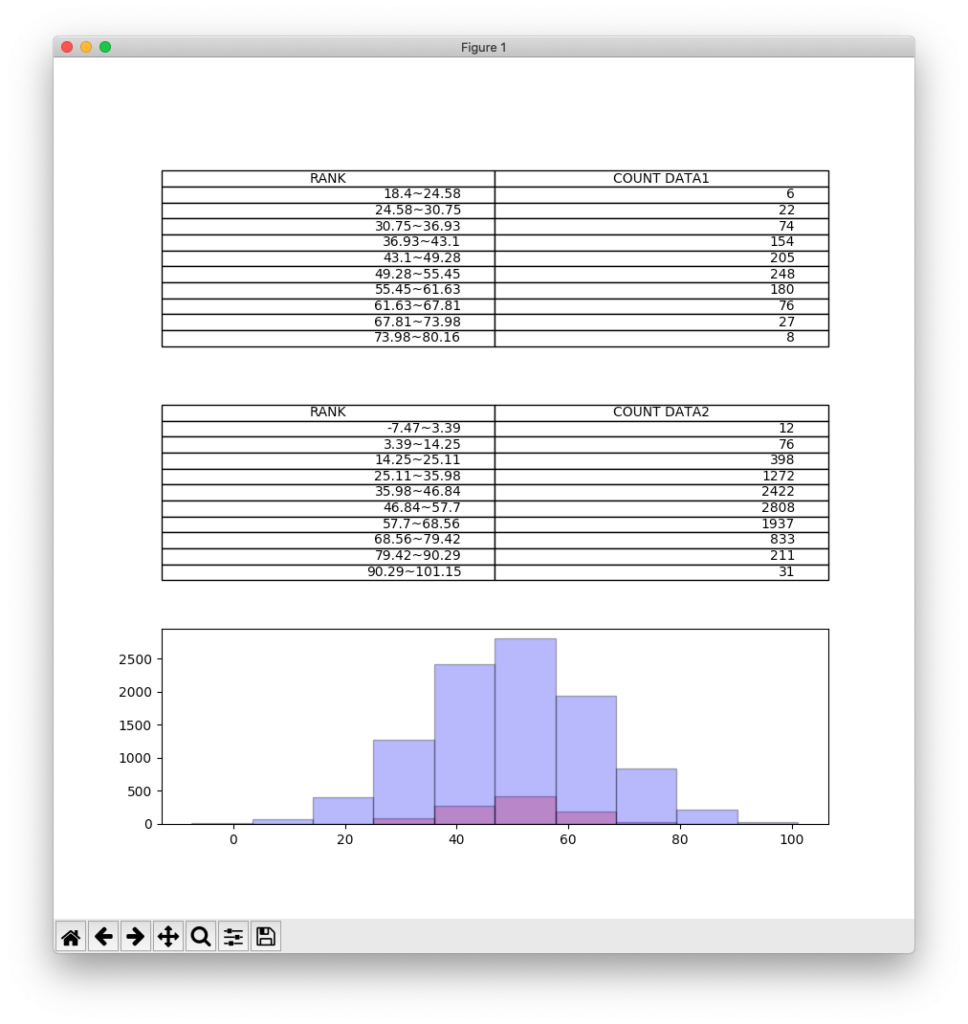
どうでしょう?度数の合計が大きく異なるため、ヒストグラムの高さも大きく差が出てしまい、分布の違いが比較しにくいですよね。このように、度数の合計が大きく異なるデータを比較する場合には相対度数を用います。相対度数とは、度数合計に対する各階級の度数の、相対比率のことです。以下の計算式で求めます。
[mathjax]$$ \frac{f_i}{n} × 100(%) $$
matplotlibのpyplot.histでは、引数にdensity=’true’を渡すことで、合計面積が1となるヒストグラムを表示してくれます。以下は相対度数によるヒストグラムを表示するコードです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data1 = np.random.normal(50, 10, 1000)
hist1, bin_edges1 = np.histogram(data1, bins=10)
data2 = np.random.normal(50, 15, 10000)
hist2, bin_edges2 = np.histogram(data2, bins=10)
data_all = np.hstack((data1, data2))
df1 = pd.DataFrame({
'RANK': [str(round(bin_edges1[i - 1], 2)) + '~' + str(round(bin_edges1[i], 2)) for i in range(1, len(bin_edges1))],
'COUNT DATA1': [hist for hist in hist1],
'RELATIVE': [round((hist / len(data1)) * 100, 2) for hist in hist1]
})
df2 = pd.DataFrame({
'RANK': [str(round(bin_edges2[i - 1], 2)) + '~' + str(round(bin_edges2[i], 2)) for i in range(1, len(bin_edges2))],
'COUNT DATA2': [hist for hist in hist2],
'RELATIVE': [round((hist / len(data2)) * 100, 2) for hist in hist2]
})
# 3行1列のグラフレイアウトを作成する
row = 3
col = 1
plt.figure(figsize=(row*3, col*9))
# 1行目にデータ1の度数分布表を描画する
plt.subplot(row, col, 1)
plt.axis('off')
plt.table(cellText=df1.values, colLabels=df1.columns, loc='center')
# 2行目にデータ2の度数分布表を描画する
plt.subplot(row, col, 2)
plt.axis('off')
plt.table(cellText=df2.values, colLabels=df2.columns, loc='center')
plt.subplot(row, col, 3)
plt.hist(data1, bins=10, range=[data_all.min(), data_all.max()], histtype='barstacked',
ec='black', alpha=0.3, color='r', density='true')
plt.hist(data2, bins=10, range=[data_all.min(), data_all.max()], histtype='barstacked',
ec='black', alpha=0.3, color='b', density='true')
plt.show()
実行すると、下記の結果が表示されます。
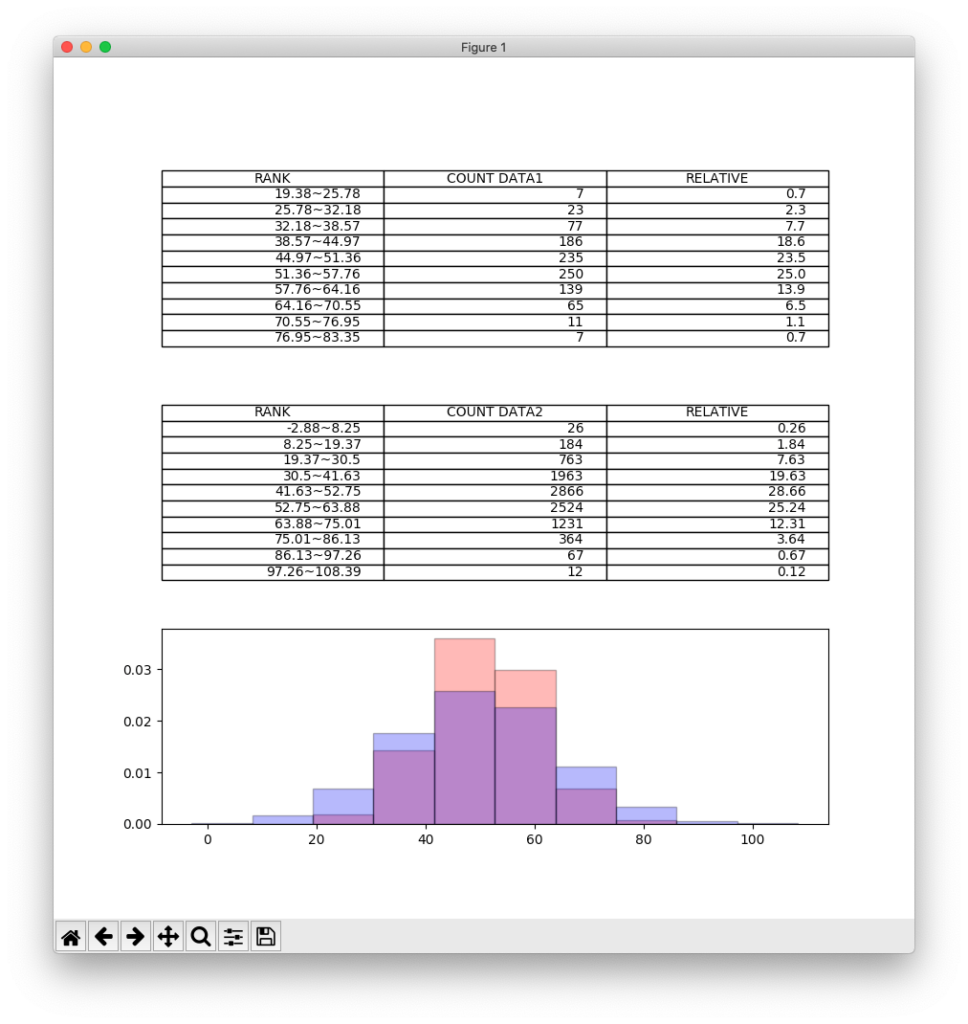
2つのデータ分布の特徴の違いが捉えやすくなったかと思います。
今回のまとめ
今回は、データの特徴を視覚的に捉えるための度数分布表とヒストグラムについて説明しました。仕事などのプレゼンでデータを用いる時、視覚的にわかりやすくするためにも、度数分布やヒストグラムはよく使用される表現方法です。
今回説明した度数分布表は、階級幅が均等に別れた物でした。しかし、実際の統計データを表現するために使用される度数分布表は、階級幅が統一されていない物が多いです。次回は、階級幅がバラバラな度数分布表について説明したいと思います。



コメント